How To Securely Share Information
12 Feb 2022We are writing a recommender system. Let’s give a typical use case.
Meet Alice, she’ll be our reference user. She rates anime, telling us if she liked them or not. We call the data we gathered here Alice’s preferences. There are of course other persons, let’s call them the Bobs. The Bobs do the same as Alice, therefore we get a lot of preference data. Based on this data, we train a machine learning model that guesses what anime Alice may like. Then, we feed back the info. Alice now has a new anime list that she’s sure she will love.
To make this design work, wee need to gather data that we can train models on. Ideally, this data would be the preferences of each user, that is the rating they gave to each movie (if they rated any movie). But we also value privacy, and we don’t want to leak our users’ information. Our goal here is to provide recommendation to our users without leaking their preferences to anyone, including ourselves.
We propose a solution based on this paper written by Bonawitz et. al..
The problem our reference paper solves
The goal of the work of Bonawitz et. al. is to train machine learning models on users’ machines in a privacy-preserving way. Each user has their own data that they do not want to reveal, but the model has to fit that data. The example they give is that of word guessing: users want to have a model that guesses the next word they are going to type, so that they can write faster, but they do not want anyone to know exactly what they are typing.
The method is designed for gradient descent: a model is trained iteratively by slowly shifting its parameters in a direction that improves its accuracy. That “direction” is the gradient that is computed at each step of the training.
The computation is distributed on users’ devices, and a central server supervises the process. For each step, each user computes their gradient, then everyone agrees on the mean value of all the individual gradients, and the server uses the result to move to the next step.

The paper of Bonawitz et. al. explains how to compute the mean of the gradients without anyone – not even the server – knowing the others’ gradients. It even goes a bit further than that: users can drop at any time during the training process, and the model will still be trained as long as a certain amount of users are still connected (this relies on secret sharing).
Using this to our advantage
What out reference paper really explains is how to securely aggregate information as long as the information can be encoded as a vector. But in computer science, everything can be seen as a vector of bits, so we can transform this method in a method to anonymously collect messages from our users.
To make an analogy, the aggregation process is like having a piece of paper and some magic ink that it is invisible until it is heated. People can write whatever they want on the paper and then reveal the result after they all finished to write. Because they use magic ink that is invisible until the paper is heated, they can’t read what the others wrote. Here, we want people to write their preferences and then reveal the list of all preferences without being able to guess the participants’ preferences.
Concretely, let’s say we have four users, Alice, Beatrice, Christine and Dominique. Let’s say their preferences can be encoded over 4 bits1, and that the encoded preference is never null. Alice and her friends will build an 8 bits long message that will contain their preferences. We use 16 bits because the final message will contain four “slots”, one for each individual message. Alice’s preferences are \({\mathtt{1001}}\), Beatrice’s are \({\mathtt{0110}}\), Christine prefers \({\mathtt{1010}}\) and Dominique votes \({\mathtt{0101}}\) (we can use any other non-null encoding).

Alice, Beatrice, Christine and Dominique just need to know where to put their individual preferences in the final vector. Let’s say Alice will take the first 4 bits, Beatrice will take the next 4 bits, and so on.
The final message will then be \({\mathtt{1001\,0110\,1010\,0101}}\), i.e., with proper notation, \((\mathtt{1001} \mathtt{<<} 12) \wedge (\mathtt{0110} \mathtt{<<} 8) \wedge (\mathtt{1010} \mathtt{<<} 4) \wedge \mathtt{0101}\). Using the technique that is explained by Bonawitz et. al., we can compute this securely2.
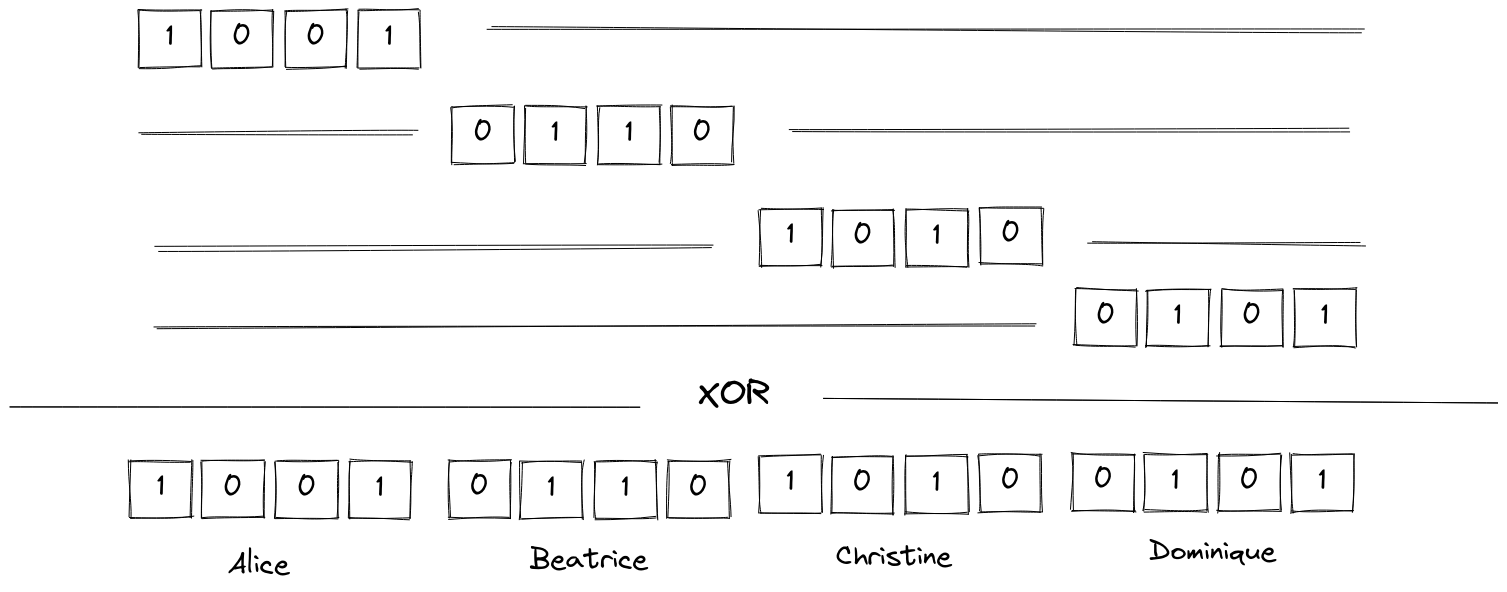
We only have one problem: how do Alice, Beatrice, Christine and Dominique know in which slot to put their preferences ? To continue the magic ink analogy, when people are writing, they don’t know if they are writing at a place where someone else already wrote. The difficulty is that they need a way to find somewhere to write, without explicitly agreeing on which part of the paper belongs to whom since knowing where people write implies knowing what they write.
So how do people know where to write without colliding with someone else’s data ? The solution is simple: they don’t! They randomly choose a place in the final vector. If two of them choose the same place, we’ll know, because the final vector will not make sense (one of the two four will be null).
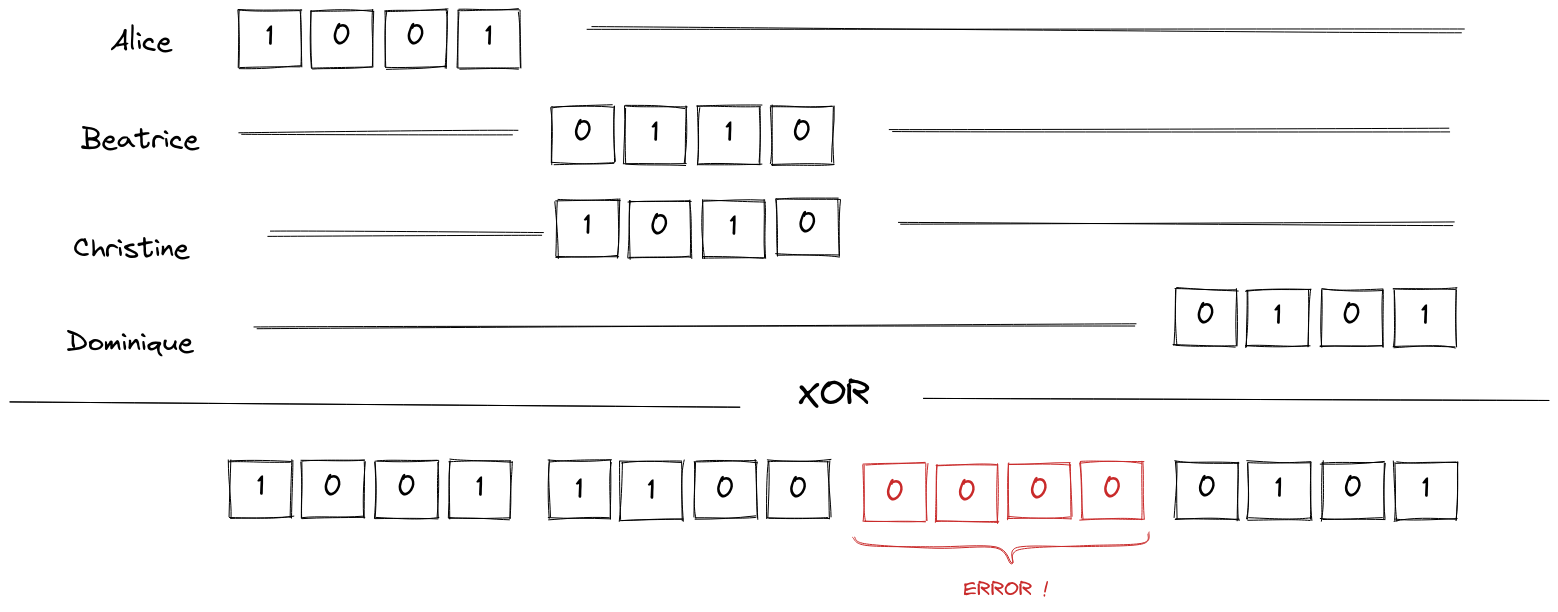
At the end, the preferences were randomly put in the final vector and no information on Alice’s, Beatrice’s, Christine’s or Dominique’s preferences has been leaked during the aggregation process. Therefore, when someone reads the final vector, they can’t know which encoded preference belongs to who: the result can be safely published without compromising the users’ privacy.
Mathematically, we were just writing about vectors over the two element field.
More detail
The previous example is, of course, degenerate, because there are only four users, and our strategy to find slots for each user is too expensive.
In practice, there are many users, therefore the only information one can ever have about the resulting dataset is that each collected preference vector belongs to some user that contributed, but no more information than that can be gathered, even by the server (except if there are many colluding users).
The problem of privately finding a slot for each user is solved by starting with simpler rounds where users try to take a random slot, represented by a bit in a giant vector, and the users agree when they see there has been no collision.
There is another problem: that of malevolent user trying to write everywhere (similar to ballot stuffing). This is sorted out by appending individual messages with hashes, so that when two messages are written in the same slot the hashed don’t match anymore.
The protocol is also made more secure by requiring key exchanges and signed transactions, so that users know that the other users they see are not dummies controlled by a malicious server. These cryptographic schemes come from libraries that are essentially built on top of curve25519 cryptography.
The protocol also uses Shamir Secret Sharing, so that if some user drops from the exchange the aggregation process can continue, as long as there are enough remaining users.
We also use ChaCha for cryptographically secure random data generation.
The libraries we used are:
Extra: An overview of the reference paper’s idea
To put the idea more formally, we have parties \(\mathcal{U}_1, \ldots, \mathcal{U}_n\) and a server \(\mathcal{S}\) communicating over some network. Each party has a vector \(v_i\). We want the server to know \(\sum_{i=1}^n v_i\) without anyone knowing (nor being able to guess) the \(v_i\).
The main idea is that a party \(\mathcal{U}_i\) won’t ever send its \(v_i\), but it will send \(v_i + w_i\) where \(w_i\) is called the individual noise vector. The security comes from the fact that the \(w_i\) will be evenly distributed over the set of all possible vectors, so \(v_i + w_i\) will be completely indistinguishable from just noise. We want to compute \(\sum_{i=1}^n v_i\), but we can only compute \(\sum_{i=1}^n v_i + w_i\). The idea is to ensure that \(\sum_{i=1}^n w_i = 0\), so that \(\sum_{i=1}^n v_i + w_i = \sum_{i=1}^n v_i\).
To get a secure \(w_i\), each pair of users agrees on a random vector they will add3 to their individual noise vector.
For even more detail, and a proof of the security of the protocol, see the paper of Bonawitz et. al.
Second extra: Closing the loop with privacy-preserving recommendation
We discussed privacy-preserving aggregation of data, and we showed we can use it to gather training data for ML models. We can go further and provide secure recommendations without leaking information about user preferences.
Let’s say we collected data and we trained an ALS model. In that case, each anime has an embedding, and each user has their own embedding too. Ratings are predicted by simple dot products \(\langle \texttt{user} \mid \texttt{anime} \rangle\). There are several possibilities for users to find their recommendations.
The first possibility is that, since each user knows where their own preferences lie in the collected data, they can download the whole model and perform the dot products themselves without the server knowing which of the collected preferences belongs to the user. This implies no more leakage of data than what we currently have.
We could also have the server publish the data of every anonymized user (publish the dot products directly), which amounts to the same, this just changes where the computation happens but not the security model.
We could also have the server publish just the embedding of every anime, and the users train their own local model. With this technique, we lose a little accuracy on the predictions, but we gain several benefits:
- The data each user has to download (the embedding of each anime) is small (the order of magnitude would be 100 kilobytes at most) compared to what they have to download with the previous solutions;
- New users who didn’t participate in the preference collection process can have ratings (since they can train their own model based on the embeddings they are given by the server);
- There is no complicated bookkeeping: users don’t have to know where their data lies in the anonymized data set.
-
4 users and 4 bits is ridiculously small, but it is easier to picture, and the example scales well ! ↩
-
We said that bit strings are vectors, and we used the exclusive or operation \(\wedge\). ↩
-
To make it work, when \(\mathcal{U}_i\) and \(\mathcal{U}_j\) agree on \(v\), \(\mathcal{U}_i\) adds \(v\) to her individual noise vector and \(\mathcal{U}_j\) adds \(-v\), so that \(v\) and \(-v\) cancel out when the final sum is computed. ↩